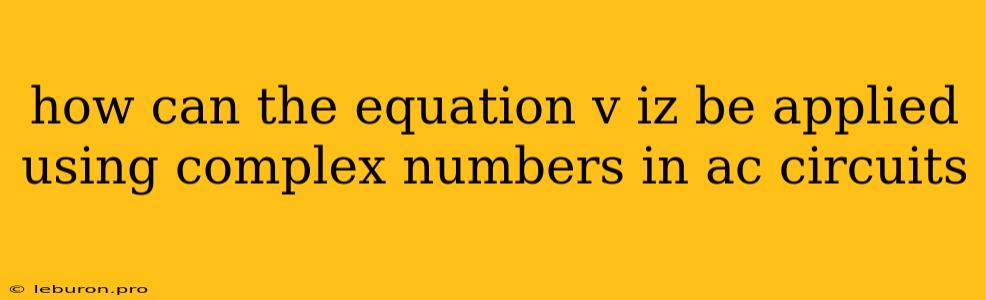The equation V = IZ, often referred to as Ohm's Law, is a fundamental concept in electrical circuits. It relates the voltage (V) across a circuit element to the current (I) flowing through it and the impedance (Z) of the element. While this equation holds true for both DC and AC circuits, its application in AC circuits becomes more nuanced due to the sinusoidal nature of voltage and current. This is where the power of complex numbers comes into play. Complex numbers provide a framework for handling the phase relationships between voltage and current in AC circuits, making the analysis of these circuits much more straightforward. In this article, we will delve into how the equation V = IZ can be effectively applied using complex numbers in AC circuits.
Understanding Impedance in AC Circuits
In DC circuits, resistance is the primary factor that impedes current flow. However, in AC circuits, the situation becomes more complex. The impedance (Z) is a generalization of resistance that encompasses not only the resistance (R) but also the reactance (X) due to capacitors and inductors. Reactance is the opposition to current flow caused by the storage of energy in electric and magnetic fields. Capacitive reactance (Xc) is inversely proportional to the frequency of the AC signal, while inductive reactance (Xl) is directly proportional to the frequency.
Complex Impedance
To account for the combined effect of resistance and reactance, we represent impedance as a complex number. The real part of the complex number represents resistance, and the imaginary part represents reactance.
Z = R + jX
Where:
- Z is the impedance (a complex number)
- R is the resistance (real part)
- X is the reactance (imaginary part)
- j is the imaginary unit (√-1)
Applying Complex Numbers in AC Circuits
Using complex numbers allows us to represent the voltage and current in AC circuits as phasors. Phasors are rotating vectors that represent the magnitude and phase angle of the sinusoidal quantities. The length of the phasor represents the amplitude, and the angle it makes with the horizontal axis represents the phase.
Voltage, Current, and Impedance Phasors
- Voltage Phasor: V = |V|∠θv
- Current Phasor: I = |I|∠θi
- Impedance Phasor: Z = |Z|∠θz
Where:
- |V|, |I|, and |Z| are the magnitudes of voltage, current, and impedance, respectively.
- θv, θi, and θz are the phase angles of voltage, current, and impedance, respectively.
Using V = IZ with Complex Numbers
Now, let's see how the equation V = IZ can be applied using complex numbers in AC circuits.
- Voltage (V): The voltage across a circuit element is the product of the current (I) flowing through it and the impedance (Z) of the element.
- Current (I): The current flowing through a circuit element is the ratio of the voltage (V) across it to the impedance (Z) of the element.
- Impedance (Z): The impedance of a circuit element is the ratio of the voltage (V) across it to the current (I) flowing through it.
Example: Analyzing an RC Circuit
Consider a simple RC circuit with a resistor (R) and a capacitor (C) connected in series. Let's assume the applied voltage is given by:
V(t) = Vm sin(ωt)
Where:
- Vm is the peak voltage
- ω is the angular frequency (2πf)
- t is time
- Find the impedance: The impedance of the RC circuit is:
Z = R + jXc = R + j(1/ωC)
- Find the current: The current in the circuit is:
I = V/Z = (Vm sin(ωt)) / (R + j(1/ωC))
- Simplify the current: To simplify the expression, we can multiply the numerator and denominator by the conjugate of the denominator:
I = (Vm sin(ωt) * (R - j(1/ωC))) / (R² + (1/ωC)²)
- Find the magnitude and phase angle of the current: The magnitude and phase angle of the current can be determined from the simplified expression.
|I| = Vm / √(R² + (1/ωC)²)
θi = -arctan(1/(ωRC))
The negative sign indicates that the current lags the voltage in an RC circuit.
Advantages of Using Complex Numbers in AC Circuits
- Simplifies calculations: Complex numbers allow us to handle the phase relationships between voltage and current in a straightforward way.
- Provides a unified framework: Complex numbers provide a consistent framework for analyzing both resistive and reactive components in AC circuits.
- Enables graphical representation: Phasors provide a graphical representation of voltage, current, and impedance, which aids in visualizing the relationships between these quantities.
Conclusion
The application of complex numbers in AC circuits significantly enhances the analysis and understanding of these circuits. By representing voltage, current, and impedance as complex numbers, we can readily account for phase relationships and simplify calculations. The equation V = IZ, when used in conjunction with complex numbers, becomes a powerful tool for analyzing and designing AC circuits. This approach allows for a deeper understanding of the behavior of AC circuits and enables engineers to optimize their design and performance.